Galois und seine legendäre letzte Nacht – Teil 1
Warum die Resultate einer schlaflosen Nacht des damals 20-jährigen Évariste Galois noch heute die Mathematik begeistern, wieso wir uns über das Lösen von Gleichungen noch heute den Kopf zerbrechen und was all das mit moderner Datenübertragung zu tun hat, ist Thema dieses Artikels in zwei Teilen.
Es war das Jahr 1832 als eines der größten Genies in der Geschichte der Mathematik im zarten Alter von 20 Jahren starb. Sein Tod war das Resultat eines Pistolenduells – ein Duell um das junge Mädchen Stéphanie-Félicie Poterin du Motel. Diesem Duell geht eine der legendärsten Nächte der mathematischen Historie vorher.
Dieses mathematische Ausnahmetalent war Évariste Galois. Warum die Resultate der schlaflose Nacht dieses damals 20-Jährigen noch heute die Mathematik begeistern, wieso wir uns über das Lösen von Gleichungen noch heute den Kopf zerbrechen und was all das mit moderner Datenübertragung zu tun hat, ist Thema dieses Artikels in zwei Teilen.
Polynomiale Gleichungen
Eine der fundamentalen Fragen der Mathematik ist welche Zahlen bestimmte Bedingungen erfüllen, wobei sich eine solche Bedingung üblicherweise in einer Gleichung formalisieren lässt. Eine typische Frage einer Mathematikprüfung könnte beispielsweise lauten:
- Für welche Werte von \(x\), gilt \(e^x=x^2\)?
Das Lösen solcher (und deutlich komplexerer) Gleichungen hat in den letzten Jahren auf den sozialen Netzwerken Konjunktur erfahren. Insbesondere auf Youtube füllen User wie Blackpenredpen und Michael Penn den Markt mit cleveren und oft überraschenden Lösungswegen für besonders kniffelige Beispiele. Auch wenn mathematische Arbeit häufig mit der Untersuchung von Beispielen beginnt, ist der Reflex des Mathematikers doch stets eine Systematisierung zur Untersuchung solcher Fragestellungen zu entwickeln.
Eine der wichtigsten Klassen von mathematischen Gleichungen ist durch sogenannten Polynome gegeben.
Definition
Ein Polynom ist ein Ausdruck \(f(x)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0\), für feste Zahlen \(a_0,\dots,a_n\). Wir nennen die größte Zahl \(l\) für die \(a_l\neq0\) den Grad und die Zahlen \(a_0,\dots,a_n\) die Koeffizienten des Polynoms.
Beispiele solcher Polynome sind Ausdrücke wie \(f(x)=x^3+x^2+2x+1\) oder \(g(x)=x^2-5x+1\) — wobei der Grad von \(f\) drei und der Grad von \(g\) zwei ist. Das Lösen von polynomialen Gleichungen, also Gleichungen der Form \(f(x)=0\) für ein Polynom \(f\), stellt eine zentrale Frage der Mathematik dar, die einigen Leser:innen insbesondere für Polynome von Grad zwei aus der Schulzeit bekannt sein wird.
Wie dies zu erwarten ist, steigt die Komplexität der Lösung solcher Gleichungen mit dem Grad der Polynome. Eine erste Beschränkung dieser Komplexität gibt das folgende klassische Resultat.
Proposition
Sei \(f\) ein Polynom von Grad \(n\). Dann hat die Gleichung \(f(x)=0\) höchstens \(n\) Lösungen.
In anderen Worten: Die Anzahl der Nullstellen eines Polynoms ist durch den Grad beschränkt. Eine weitere elementare Frage ist, welche polynomialen Gleichungen überhaupt Nullstellen im vorgegebenen Zahlenraum besitzen. Beispielsweise hat die Gleichung \(x^2-2=0\) keine Lösung über den rationalen Zahlen, also den Zahlen der Form \(\frac{a}{b}\) für zwei natürliche Zahlen \(a,b\) und \(b\neq0\). Erweitert man den Zahlenraum auf den der reellen Zahlen, hat die Gleichung genau zwei Lösungen, nämlich \(x_1=\sqrt{2}\) und \(x_2=-\sqrt{2}\). Die geneigten Leser:innen mögen nun der Vermutung verfallen, dass jede polynomiale Gleichung über den reellen Zahlen lösbar ist, in welchem Fall die eben vorgenommen Einschränkung auf die rationalen Zahlen artifiziell erscheinen mag. Diese Leser:innen werden jedoch schnell entäuscht, denn eine kurze Betrachtung des Polynoms \(f(x)=x^2+1\) führt zu der Beobachtung, dass die Gleichung \(f(x)=0\) keinerlei Lösung über den reellen Zahlen besitzt — dies ist der Tatsache geschuldet, das das Quadrat einer reellen Zahl nicht-negativ ist.
Das Wesen von Nullstellen von Polynomen ist also diffus, aber auch höchst interessant. Es ist die Grundlegung zu einer systematischen Untersuchung dieses Wesens, die Évariste Galois berühmt machte und das noch heute aktiv beforschte mathematische Gebiet der Galois Theorie begründete.
Der Legende nach ereigenete sich in der Nacht vor Galois‘ Tod Dramatisches. Getrieben von der Überzeugung seines bald nahenden Todes, soll das junge Genie seine letzten Stunden genutzt haben, um seinen mathematischen Ergebnisse zu verschriftlichen. In einem Brief, der seine Ideen skizzierte, entschuldigte er dessen unvollständige Ausführung mit der Randnotiz:
„Je n’ai pas le temps.“
übersetzt: Ich habe keine zeit.
Dieser Brief sollte die Grundlage für ein gesamtes mathematisches Forschungsgebiet legen.
Auch wenn sich die Dramaturgie von Galois‘ letzten Stunden bei genauer historischer Betrachtung nicht aufrecht erhalten lässt und seine Manuskripte schon in den Monaten zuvor Teilen der mathematischen Gemeinschaft zur Verfügung standen, ist dieser berühmte Brief eines der einflussreichsten wissenschaftshistorischen Dokumente der Menschheitsgeschichte.
Nach diesem historischen Diskurs, stellt sich natürlich die Frage, welche Überlegungen nun den Weg in diesen Brief fanden. Um dies zu erklären müssen wir uns zunächst mit dem Begriff der Symmetrie befassen.
Symmetrien und Gruppen
Symmetrien sind seit je her ein Begriff des Alltags und auch alle Leser:innen haben vermutlich zumindest eine vage Vorstellung davon was mit diesem Begriff gemeint ist. Gerade diese Alltäglichkeit des Begriffs Symmetrie, macht es zu einer besonders spannenden Frage, wie man ihn mathematisch formalisieren sollte. Eine Art der Formalisierung ist durch das Konzept der „Gruppe“ gegeben, wobei der Begriff „Gruppe“ wohl auf Galois selbst zurückgeht.
Um dieses Konzept zu erläutern, beschäftigen wir uns zunächst mit einem Beispiel: Dem Dreieck. Wir betrachten das folgende gleichseitige Dreiecke, dessen Kanten die Länge \(1\) haben und dessen Ecken wir mit \(A,B,C\) bezeichnen.

Was sind nun die „Symmetrien“ des Dreiecks? Unter einer Symmetrie verstehen wir mathematisch eine Transformation, die das Dreieck in sich selbst überführt. Die einfachste Symmetrie ist also die Transformation, die das Dreieck nicht bewegt. Diese nennen wir die Identität, die wie wir mit \(I\) bezeichen. Eine etwas spannendere Symmetrie ist gegeben durch die hier eingezeichnete Spiegelung, die die Ecken \(A\) und \(B\) vertauscht, die wir \(S(A,B)\) nennen.

Analog betrachten wir die Spiegelung, welche die Ecken \(A\) und \(C\) vertauscht, die wir \(S(A,C)\) nennen und die Spiegelung, die die Ecken \(B\) und \(C\) vertauscht, die wir \(S(B,C)\) nennen.

Eine weitere Klasse von Symmetrien ist durch Rotationen gegeben. Rotiert man das Dreieck um 120° gegen den Uhrzeigersinn um den Mittelpunkt des Dreiecks, so wird das Dreieck in sich selbst überführt wobei die Ecke \(A\) den Platz der Ecke \(B\) einnimmt, die Ecke \(B\) den Platz der Ecke \(C\) und die Ecke \(C\) den Platz der Ecke \(A\). Wir nennen die Rotation um 120° \(R(120)\).
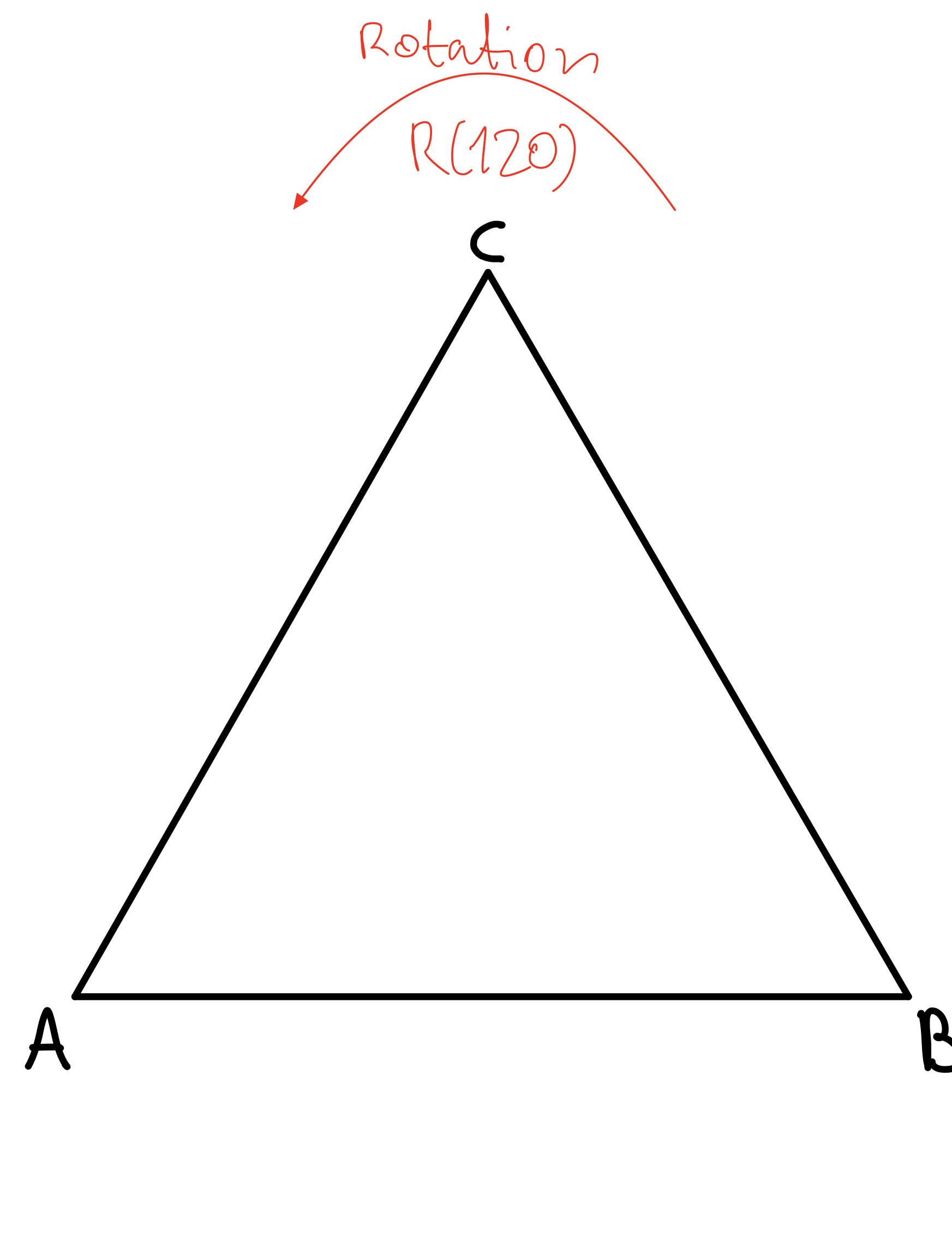
Nun betrachten wir Rotation des Dreiecks um 240° gegen den Uhrzeigersinn um den Mittelpunkt des Dreiecks. Auch diese Rotation überführt das Dreieck in sich selbst, wobei die Ecke \(A\) die Position der Ecke \(C\) einnimmt, die Ecke \(B\) die Position der Ecke \(A\) und die Ecke \(C\) die Position der Ecke \(B\). Wir bennen die Rotation um 240° mit dem Symbol \(R(240)\).
Es stellt sich heraus, dass dies alle Symmetrien des Dreiecks sind:
- Die Identität \(I\).
- Die Spiegelung \(S(A,B)\), die die Ecken \(A\) und \(B\) vertauscht.
- Die Spiegelung \(S(A,C)\), die die Ecken \(A\) und \(C\) vertauscht.
- Die Spiegelung \(S(B,C)\), die die Ecken \(B\) und \(C\) vertauscht.
- Die Rotation \(R(120)\), die das Dreieck 120° gegen den Uhrzeigersinn rotiert.
- Die Rotation \(R(240)\), die das Dreieck 240° gegen den Uhrzeigersinn rotiert.
Die Hintereinanderausführung von Symmetrien ist wiederum eine Symmetrie. Beispielsweise sehen wir, dass die zweifache Ausführung der Spiegelung \(S(A,B)\) das Dreieck wieder in einen Ursprungszustand versetzt, also der Identität entspricht — symbolisch drücken wir dies durch \(S(A,B)\circ S(A,B)=I\). Eine interessante Verkettung von Symmetrien ergibt sich, wenn wir zunächst die Spiegelung \(S(B,C)\) und dann die Spiegelung \(S(A,B)\) anwenden. Wie wir im folgenden Bild sehen, ergibt sich daraus die Rotation um 120° — in Symbolen \(S(A,B)\circ S(B,C)=R(120)\).

Es sei den geneigten Leser:innen überlassen sich zu überzeugen, dass sich alle sechs Symmetrien aus der Spiegelung \(S(A,B)\) und der Rotation \(R(120)\) erzeugen lassen.
Dieses Beispiel wollen wir nun abstrahieren. Wie wir gesehen haben, hat das Dreieck sechs Symmetrien, denen wir Symbole zugeordnet haben. Diese Symmetrien lassen sich wiederum verketten und diese Verkettung ergibt wieder ein Symmetrie. Alle möglichen Verkettung sammeln wir in der folgenden Tabelle, wobei der Eintrag in der Zeile von \(\bf S(A,B)\) und in der Spalte von \(\bf S(A,C)\) die Verkettung \(S(A,B)\circ S(A,C)\) repräsentiert. In anderen Worten, korrespondiert dieser Eintrag zu der Symmetrie, die wir erhalten, wenn wir zunachst die Spiegelung \(S(A,C)\) auf das Dreieck anwenden und dann die Spiegelung \(S(A,B)\).
| \(\circ\) | \(\bf I\) | \(\bf S(A,B)\) | \(\bf S(A,C)\) | \(\bf S(B,C)\) | \(\bf R(120)\) | \(\bf R(240)\) |
| \(\bf I\) | \( I\) | \( S(A,B)\) | \( S(A,C)\) | \( S(B,C)\) | \( R(120)\) | \(R(240)\) |
| \(\bf S(A,B)\) | \( S(A,B)\) | \( I\) | \(R(240)\) | \( R(120)\) | \( S(B,C)\) | \( S(A,C)\) |
| \(\bf S(A,C)\) | \( S(A,C)\) | \(R(120)\) | \( I\) | \(R(240)\) | \( S(A,B)\) | \( S(B,C)\) |
| \(\bf S(B,C)\) | \( S(B,C)\) | \(R(240)\) | \( R(120)\) | \( I\) | \( S(A,C)\) | \( S(A,B)\) |
| \(\bf R(120)\) | \(R(120)\) | \(S(A,C)\) | \( S(B,C)\) | \( S(A,B)\) | \(R(240)\) | \( I\) |
| \(\bf R(240)\) | \( R(240)\) | \(S(B,C)\) | \( S(A,B)\) | \( S(A,C)\) | \( I\) | \( R(120)\) |
Diese Tabelle nennt man die Symmetriegruppe des Dreiecks. Analog erhalten wir Symmetriegruppen für andere geometrische Objekte wie Quadrate, Würfel oder Pyramiden. Diese Symmetriegruppen sind das Herz von Galois‘ Untersuchung der Lösungen polynomialer Gleichungen.
Symmetriegruppen von Gleichungen und der Satz von Abel-Ruffini
Kommen wir nun zurück zu unserem ursprünglichen Ziel, nämlich der Untersuchung der Lösungsmenge \(f(x)=0\) für ein Polynom \(f\). Um Galois‘ Ansatz zu verstehen, beschäftigen wir uns zunächst mit dem Polynom \(f(x)=x^2-2\).
Wie schon weiter oben besprochen, besitzt die polynomiale Gleichung \(x^2-2=0\) keine Lösungen in den rationalen Zahlen — wie mathematisch üblich bezeichnen wir im Folgenden die rationalen Zahlen mit \(\mathbb{Q}\) bezeichnen. Des Weiteren haben wir bereits festgestellt, dass nach Erweiterung des Zahlenraums auf die reellen Zahlen, diese Gleichung zwei Lösungen besitzt, nämlich \(x_1=\sqrt{2}\) und \(x_2=-\sqrt{2}\). Nach der Diskussion im letzten Kapitel, beobachten sofort eine gewisse Symmetrie dieser Lösungen: Multiplizieren wir \(x_1\) mit \(-1\) erhalten wir \(x_2\) und multiplizieren wir \(x_2\) mit \(-1\) erhalten wir \(x_1\). Dies wollen wir nun als Symmetriegruppe dieser Lösungsmenge auffassen. Zusätzlich zu dieser Symmetrie, die wir durch Multiplikation mit \(-1\) und mit \(M\) bezeichnen, gibt es noch die triviale Symmetrie, die \(x_1\) und \(x_2\) invariant lässt, also die Identität \(I\). Die korrespondierende Tabelle ist die folgende.
| \(\circ\) | \(\bf I\) | \(\bf M\) |
| \(\bf I\) | \(I\) | \(M\) |
| \(\bf M\) | \(M\) | \(I\) |
Dies ist die Symmetriegruppen der folgende Gerade, wobei \(I\) zur Identität, als zu der Transformation, die die Gerade festhält korrespondiert und \(M\) zur eingezeichneten Spiegelung.

Die zentrale Erkenntnis für die Galois Theorie, die nach Kenntnis des Autors dieses Artikels auf eine Arbeit des Mathematikers Joseph-Louis Lagrange aus dem Jahr 1770 zurückgeht, ist, dass jedem Polynom über den rationalen Zahlen eine solche Symmetriegruppe kanonisch zugeordnet werden kann. Beispielsweise ist die Symmetriegruppe des Polynoms \(f(x)=x^3-2\) genau die Symmetriegruppe des Dreiecks. Es war die Konzeptualisierung der Untersuchung der Lösungsmenge eines Polynoms durch diese Symmetriegruppen, die Galois unsterblich machten.
Um Galois‘ Motivation zu verstehen, ist es zentral den mathematisch-historischen Kontext seiner Arbeit zu betrachten. Die Lösung polynomialer Gleichungen bis zu Grad vier war im 16. Jahrhundert verstanden. Für Grad zwei mag dies einigen Leser:innen aus der Schulzeit bekannt sein in Form der sogenannten Mitternachtsformel, die besagt, dass die Nullstellen eines Polynoms \(f(x)=x^2+px+q\) gegeben sind durch \(x_1=-\frac{p}{2}+\sqrt{\frac{p^2}{4}-q}\) und \(x_2=-\frac{p}{2}-\sqrt{\frac{p^2}{4}-q}\). Ähnliche Formeln existieren für Grad drei und vier. All diese Formeln drücken die Nullstellen durch Ausdrücke in den Koeffzienten mittels Addition, Subtraktion, Multiplikation, Division und Wurzeln aus. Die Frage, ob eine solche Formel auch für Grad fünf oder größer existiert, blieb bis zum Jahr 1824 ungelöst, als der Mathematiker Niels Henrik Abel aufbauend auf einem unvollständigen Beweis des Mathematikers Paolo Ruffini aus dem Jahr 1799, den folgenden Satz zeigte, welcher heute als der Satz von Abel-Ruffini bekannt ist.
Satz von Abel-Ruffini
Für fast alle Polynome vom Grad fünf existiert keine Formel, die die Nullstellen nur durch Addition, Subtraktion, Multiplikation, Division und Wurzeln in den Koeffizienten ausdrückt.
Andererseits gibt es Polynome vom Grad \(5\), für die eine solche Formel existiert, wie beispielsweise \(f(x)=(x-1)^5\), dessen einzige Nullstelle \(x_1=1\) ist. Galois‘ Beobachtung war nun, dass die Frage, ob die Lösungen einer polynomialen Gleichung durch Addition, Subtraktion, Multiplikation, Division und Wurzeln ausdrückt werden können, äquivalent zu einer Eigenschaft der assoziierten Symmetriegruppe ist. Konkret zeigte Galois den folgenden revolutionären Satz.
Satz (Galois)
Die Nullstellen eines Polynoms können genau dann durch Addition, Subtraktion, Multiplikation, Division und Wurzeln in den Koeffizienten ausgedrückt werden, wenn die Symmetriegruppe des Polynoms bestimme Untersymmetriegruppen enthält.
Dieser Satz kann wie folgt umformuliert werden: Eine Formel für die Nullstellen eines Polynoms existiert genau dann, wenn die Tabelle der assoziierten Symmetriegruppe sukzessive in bestimmte kleinere Tabellen von kleineren Symmetriegruppen verfeinert werden kann. Damit gelang es Galois, die Lösbarkeitsfrage von Polynomen vollständig in das mathematische Gebiet der Gruppentheorie zu verschieben.
Kaum eine Technologie zwingt uns die Grenzen der Freiheit in einer digitalen Welt neu zu denken wie die moderne Datenübertragung. Was Galois‘ Überlegungen damit zu tun haben und was lineares Network Coding bedeutet, wird Thema des zweiten Teils sein…
Quellen
Stewart, I.N., 2015. Galois theory. CRC press.
Rothman, T., 1982. Genius and biographers: the fictionalization of Evariste Galois. The American Mathematical Monthly, 89(2), pp.84-106.


